A Fibonacci sorozat története nem a XII. és XIII. század fordulóján élt itáliai matematikussal kezdődött, hiszen sokkal korábban megtalálható az óind matematikában. Pontos írásos feljegyzése is Fibonacci felfedezése előtt 50 évvel korábban történt Indiában.
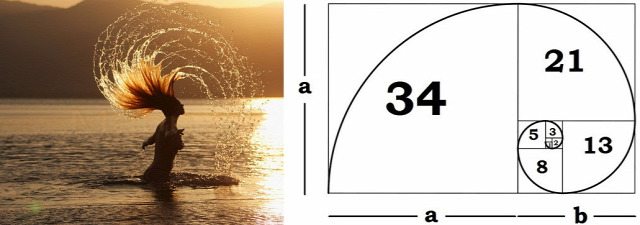
Ez a számsor kapcsolódik az emberi és isteni képzőművészethez is. Ismert neve: aranymetszés, az isteni arány. Aranymetszés, mint matematikai sorozat, mint Fibonacci számok? Érdemes körüljárni, már csak azért is, mert a számtani sorozatok misztikája már ősidőktől fogva rabul ejtette az embert. Az aranymetszés aránya, és a Fibonacci sorozat számtalan helyen fellelhető a természetben, talán ezért is varázsol el bennünket a matematikai érdekességek teremtő ereje.
Matematikai érdekességek: számtani sorozatok
Számtani sorozatról akkor beszélünk, ha egy legalább három számból álló sorozatban a második elemtől kezdve bármelyik tag és az azt megelőző tag különbsége állandó. A legegyszerűbb példa a természetes számok sorrendje, ahol mindig 1-et kapunk, ha kivonjuk a megelőző számot. (0,1,2,3,4,5…)
Felfedezőjéről szokták elnevezni, de ez sajnos nem minden esetben korrekt.
Mint látni fogjuk, a Fibonacci sorozatnál sem érvényes. Bár az itáliai matematikus nevéhez kapcsolódik, nem ő az első, aki használta ezeket a számokat. Ha egymástól függetlenül fedezték volna fel többen, még akkor is az az általános szabály, hogy annak a személynek a neve jelzi, aki az első volt. Miért fontos ez? Az indiai származású professzor, Manjul Bhargava a matematikai Nobel-díjnak megfelelő Fiedels érem kitüntetettje. Ő adta meg a választ, amikor kissé szomorkásan megjegyezte:
Bár a világon minden komoly szakember tudja, hogy ezt a sorozatot Indiában találták meg, ezt a büszkeséget elvették az indiaiaktól.
Szerencsére van jó példa is. A Mádhava-Gregory-sor is egy matematikai sorozat, melyet a 14. században fedezett fel egy szintén indiai tudós. Szangamagrámi Mádhava a Kerala iskola alapítója, csillagász és matematikus volt. Amire ő rájött, 1668-ban újra felfedezte James Gregory, skót matematikus, és tőle függetlenül Leibniz. S bár Mádhava két évszázaddal korábban már ismerte, mégis sok évnek kellett eltelnie, hogy az ő neve kerüljön a matematikai fogalom elé. Ma már elismeri a Nemzetközi Matematika Tanács, de ha megnézzük a mai szócikkeket, még mindig sok helyen hiányzik a neve, csak Gregory-sorként olvasható vagy mindkét néven, pedig valójában a 200 év jogosulttá tenné, hogy Mádhava-sorként szerepeljen…
A sorozat érdekessége, hogy a pí értékének meghatározására alkalmas, amit szintén India adott át az ókorban, s görög közvetítéssel került tovább.
Ha már Keralában járunk, még egy matematikai érdekességet érdemes megemlíteni: A Mádhava-Newton-sor a szinusz és koszinusz értékek közelítésére vonatkozik. Mádhava fedezte fel 300 évvel Newton előtt! Mégsem csak az ő neve szerepel…
A Fibonacci sorozat
A Fibonacci sorozat első két alkotórésze a 0 és az 1, a harmadik elemtől kezdve minden szám az előző kettő összege: 0, 1 – 1, 2, 3, 5, 8, 13 és így tovább. Fibonacci számok végtelen, növekvő sorozatot alkotnak. Nem véletlenül ez az egyik legismertebb számsor, hiszen a Fibonacci számok különlegessége több területet is összekapcsol. Mint ahogy látni fogjuk, ez az arány megtalálhatóak a növény- és állatvilágban, illetve az emberi testben is.
A Fibonacci sorozat egyre nagyobb sorszámú elemeinek hányadosa egy állandó számhoz, az aranymetszéshez tart. Már az ókori görögök is ismertek, és aranymetszésnek, „isteni aránynak” hívták. Egyensúlyt alkot a szimmetria és asszimmetria között. Az aranymetszés egy szakaszt úgy bont két részre, hogy a kisebbik rész úgy aránylik a nagyobbhoz, mint a nagy az egészhez. Ezt a bűvös arányt pedig a természetben és az emberi alkotásokban, az építészetben, a képzőművészetben és a zenében egyaránt megtaláljuk. Ma Fibonacci számok jelennek meg számítógépes algoritmusokban, a nyomdászatban és a tőzsdei és gazdasági stratégiák is élnek vele.
A Fibonacci sorozat története
A Fibonacci sorozat az indiai matematikában a szanszkrit prozódia kapcsán jelenik meg.
Az úgynevezett Fibonacci számok először „matrameru” (a ritmus hegye) néven szerepelnek a szanszkrit nyelvész és matematikus, Pingala Chandah-sásztra (A prozódia művészete) című munkájában.
A prozódia rendkívül fontos volt az ókori indiai rituálékban, mert a hangsúly őrizte a kimondott mantra tisztaságát.
Pingala i.e. 500 körül élt, említett műve egyben a bináris számrendszer első ismert leírása is. Halayudha írt egy kommentárt ehhez, melyben szerepel a később Pascal-háromszögként elnevezett formula, holott ő már évszázadokkal Pascal előtt tanulmányozta azt. Jelezte, hogy a „ferde” átlók tagjainak összege a Fibonacci-számokat adja. A következő nyom a 6. századi matematikus, Virahanka munkája, aki a hosszú és rövid szótagokat elemezte, itt is szerepel ez a számsor. Ezt követi Gopala és Hemachandra, akik kifejezetten megemlítik a számokat.
Hemachandra (1089-1172) dzsain tudós, költő és polihisztor volt, akit a kortársai csodagyerekként tiszteltek, és a kalikála-sarvajna, „mindentudó a Kali-júgában” címet adományozták neki, vagyis korának legbölcsebb személyiségének tartották. Nem csak csodálatos író és költő volt, aki több ezer verset komponált, egyben a logika tudományának embereként is tisztelték, aki a szerteágazó indiai filozófiai iskolák mindegyikét ismerte. Hatására Gujaratban a dzsainizmus hivatalos vallássá vált, és az állam területén betiltották az állatok levágását. Élete alkonyán hat hónappal előre bejelentette a halálát, és böjttel készült fel rá az utolsó napokban.
Hemachandra és mestere, Gopala azt is vizsgálta, hogy a rövid és hosszú szótagok miként töltenek ki egy adott időtartamot a szanszkrit költészetben. Így fedezték fel a matematikai sorozatot, melynek első pontos említése 1150-ből való.

1202-ben tőlük függetlenül találta meg Leonardo Pisano, ismertebb nevén Fibonacci, a középkor legtehetségesebb nyugati matematikusa. Akkoriban még a római számokat használták, amely igencsak megnehezítette a számolást. A fiatal Fibonacci apjával beutazta egész Észak-Afrikát. Algériában találkozott a hindu-arab számírással, és az arabok által használt tízes számrendszerrel, mellyel sokkal egyszerűbben végezhető minden számtani művelet.
Megtanulta a hindu/arab számrendszert, s számos vezető arab matematikustól tanult. Nagyrészt neki köszönhetjük, hogy az arab közvetítéssel elterjedő tízes számrendszert és az „arab”, helyesen hindu számokat Európában meghonosította. Ismereteit Liber Abaci, Könyv a számtanról című munkájában foglalta össze. Bemutatta az úgynevezett „modus Indorum”-ot (az indiaiak módszerét), amit ma hindu-arab számrendszernek nevezünk, a számjegyeket 0-9-ig, valamint a helyiérték fogalmát:
„Van tíz hindu jel: 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. Ezen jelek segítségével bármilyen számot fel lehet írni, amit csak akarunk”
– írta könyvében.
Itt található az a bizonyos, azóta szinte misztikussá váló számsor, amit róla neveztek el.
A Fibonacci sorozat a természetben
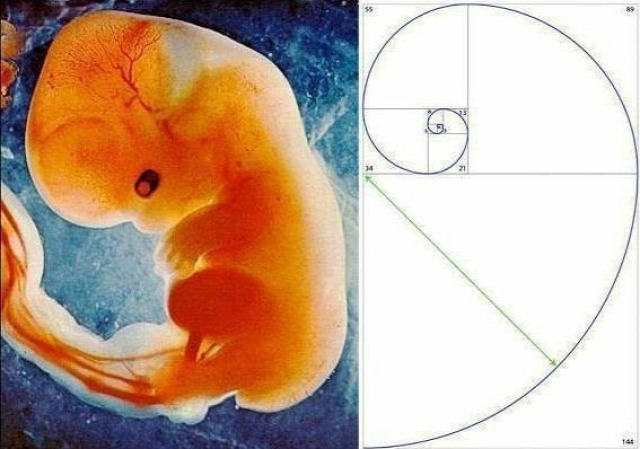
Kepler a The Six-Cornered Snowflake c. könyvében (1611) a Fibonacci számokkal kapcsolatban különféle természeti jelenségeket említ. A tudósok évszázadok óta elgondolkoztak azon, miért olyan sok természetes mintában tükröződik a Fibonacci-sorozat vagy a kezdő képen is látható Fibonacci-számok alkotta spirál.
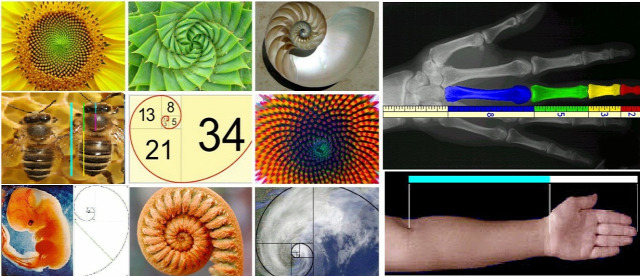
2 kezünk van, amelyek mindegyikén 5 ujj, valamennyi 3 részből áll. Az ujjak, valamint a kéz, az alkar és a kar aránya szintén erre utal. Nagyon ritka és speciális virág az, amelyiknél a szirmok száma nem egy Fibonacci-szám. A fej-tor-potroh aránya, a delfinek testfelépítése stb. Lehetetlen mindet felsorolni. Mi a helyzet az almával, a virágjának szirmával, vagy ha nem függőlegesen vágjuk ketté? Meglepetés! 5 – Fibonacci szám.
Még a mikroszkopikus birodalom sem immunis a Fibonacci-számtól: a DNS-molekula 34 angström hosszú és 21 angström széles. Ezek a Fibonacci-sorozat számai, és arányuk (1,619 ) szinte teljesen megegyezik az aranymetszés arányszámával (1,618).
Fibonacci-spirál szerint rendeződnek a fenyőtoboz vagy az ananász pikkelyei, de a napraforgó tányérja is nagyszerű példa.
Számtani sorozatok misztikája
Úgy tűnik, a Fibonacci számok alátámasztják Galilelo Galileo híres kijelentését:
„A természet nagy könyve a matematika nyelvén íródott”.
Bár az is igaz, olyan példákat is felhozhatunk, ahol nem találjuk meg ezt a sotozatot. Vannak más, szintén igen gyakori matematikai struktúrák is az élő és az élettelen természetben, ezek egyike a Voronoj-féle cellaszerkezet. A szitakötő szárnyának mintázata ez alapján épül fel.
A számok és a természet összefüggései nemcsak a matematika iránt érdeklődőknek lehet izgalmas. Ha nyitott szemmel járunk a világban, akkor a tények mögött mindig felfedezhetünk más, fontos információt is. Ez igaz a Fibonacci sorozattal kapcsolatban is.
A természet tökéletességének meglátása és az ember vágya a tökéletes kompozíció megalkotására mindig is az isteni harmónia felé terelte, vonzotta az egyént. Így az „isteni arány” varázsa nem korlátozódik a matematikára. Biológusok, képzőművészek, zenészek, történészek, építészek, pszichológusok egyaránt kutatták titkát. A matematika történetében nincs még egy ilyen fogalom, mely ennyi gondolkodót inspirált volna.
A matematikai érdekességek teremtő ereje
Marcus Du Sautoy, az Oxfordi Egyetem matematika professzora néhány éve Indiában forgatott dokumentumfilmet (ez a youtube-on is látható). Munkájával kapcsolatban kijelentette:
„Sok ember úgy gondolja, hogy a matematika nyugati találmány volt. Ez a program arról szól, hogy egy csomó dolgot már megalkottak Indiában, mielőtt felfedezték volna a nyugati világban. Ez a munkám tehát valójában politikai is, mert azt mutatja, hogy mennyire figyelmen kívül hagyjuk Kelet felfedezéseit.”
Elmulasztunk megemlíteni mást is. A Fibonacci sorozat vagy a vele kapcsolatos aranymetszés a természetben csak véletlen egybeesés lenne? Örömmel fedezzük fel az aranymetszés, az arany arány szépségét Leonardo da Vinci műveiben vagy Le Corbusie épületeiben stb. Megnevezzük a festőket, építészeket, a műremekek alkotóit, mérnökeit.
A matematikai érdekességek teremtő ereje jól nyomon követhető Cristóbal Vila kisfilmjében is, aki remek példákat hoz a természetben előforduló, matematikailag leírható mintázatokra. Ugyanakkor hajlamosak vagyunk elfeledkezni arról a mérnökről, aki mind a mai napig sokkal tökéletesebb és változatosabb formákban mutatja meg az arany arányt.
Kapcsolódó írások








